目录
什么是机器学习
机器学习是从数据中自动分析获得规律(模型),并利用规律对未知数据进行预测
可用数据集
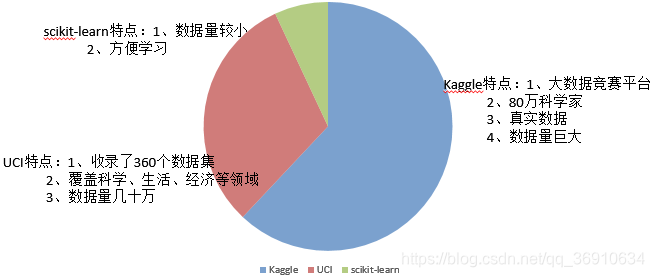
Kaggle网址:https://www.kaggle.com/datasets
UCI数据集网址: http://archive.ics.uci.edu/ml/
scikit-learn网址:http://scikit-learn.org/stable/datasets/index.html#datasets
常用数据集数据的结构组成
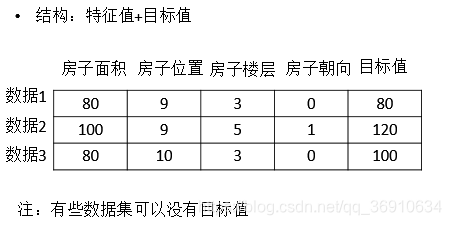
特征工程是什么
特征工程是将原始数据转换为更好地代表预测模型的潜在问题的特征的过程,从而提高了对未知数据的模型准确性
特征工程的意义
直接影响模型的预测结果
sklearn特征抽取API
sklearn.feature_extraction
字典特征抽取
作用:对字典数据进行特征值化
类:sklearn.feature_extraction.DictVectorizer
DictVectorizer语法
•DictVectorizer.fit_transform(X)
•X:字典或者包含字典的迭代器
•返回值:返回sparse矩阵
•DictVectorizer.inverse_transform(X)
•X:array数组或者sparse矩阵
•返回值:转换之前数据格式
•DictVectorizer.get_feature_names()
•返回类别名称
•DictVectorizer.transform(X)
•按照原先的标准转换
- from sklearn.feature_extraction import DictVectorizer
-
- def dictvec():
- """
- 字典数据抽取
- :return:
- """
- # 实例化
- dict = DictVectorizer(sparse=False)
-
- # 调用fit_transform把数据输入进去,直接转换成特征抽取之后的数据
- data = dict.fit_transform([{'city': '北京','temperature': 100}, {'city': '上海','temperature':60}, {'city': '深圳','temperature': 30}])
- print(dict.get_feature_names())
- print(data)
- return None
-
- if __name__ == "__main__":
- dictvec()

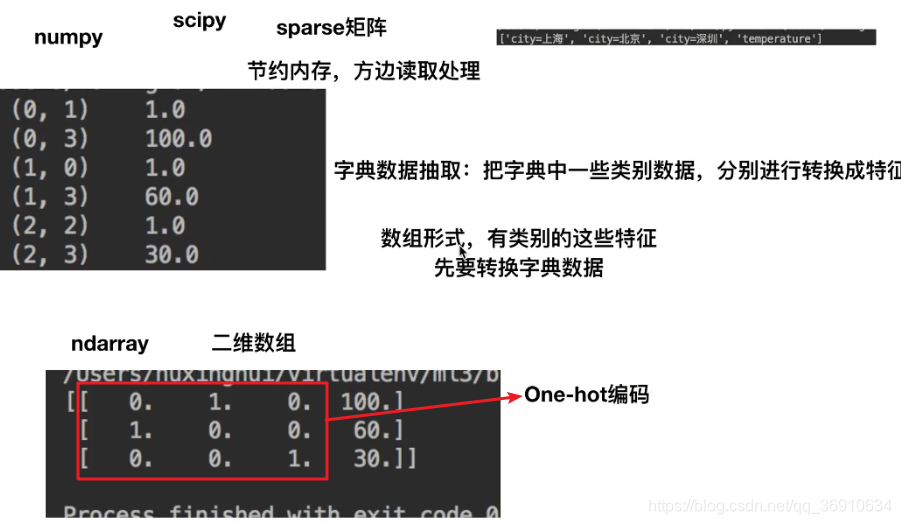
文本特征抽取
作用:对文本数据进行特征值化
类:sklearn.feature_extraction.text.CountVectorizer
CountVectorizer语法
•CountVectorizer(max_df=1.0,min_df=1,…)
•返回词频矩阵
•CountVectorizer.fit_transform(X,y)
•X:文本或者包含文本字符串的可迭代对象
•返回值:返回sparse矩阵
•CountVectorizer.inverse_transform(X)
•X:array数组或者sparse矩阵
返回值:转换之前数据格式
•CountVectorizer.get_feature_names()
•返回值:单词列表
- def countvec():
- """
- 对文本进行特征值化
- :return:
- """
- cv = CountVectorizer()
- data = cv.fit_transform(["life is short,i like python","life is too long,i dislike python"])
-
- print(cv.get_feature_names())
- print(data.toarray())
-
- return None
-
-
- if __name__ == "__main__":
- countvec()

如何去对中文文本特征值化
•import jieba
•jieba.cut(“我是一个好程序员”)
•返回值:词语生成器
- def cutword():
-
- con1 = jieba.cut("今天很残酷,明天更残酷,后天很美好,但绝对大部分是死在明天晚上,所以每个人不要放弃今天。")
-
- con2 = jieba.cut("我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。")
-
- con3 = jieba.cut("如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。")
- # print(type(con1)) <class 'generator'>
- # 转换成列表
- content1 = list(con1)
- content2 = list(con2)
- content3 = list(con3)
-
- # 把列表转换成空格隔开字符串
- c1 = ' '.join(content1)
- c2 = ' '.join(content2)
- c3 = ' '.join(content3)
-
- return c1, c2, c3
-
- def hanzivec():
- """
- 中文特征值化
- :return: None
- """
- c1, c2, c3 = cutword()
-
- print(c1, c2, c3)
-
- cv = CountVectorizer()
-
- data = cv.fit_transform([c1, c2, c3])
-
- print(cv.get_feature_names())
-
- print(data.toarray())
-
- return None
-
-
-
- if __name__ == "__main__":
- hanzivec()

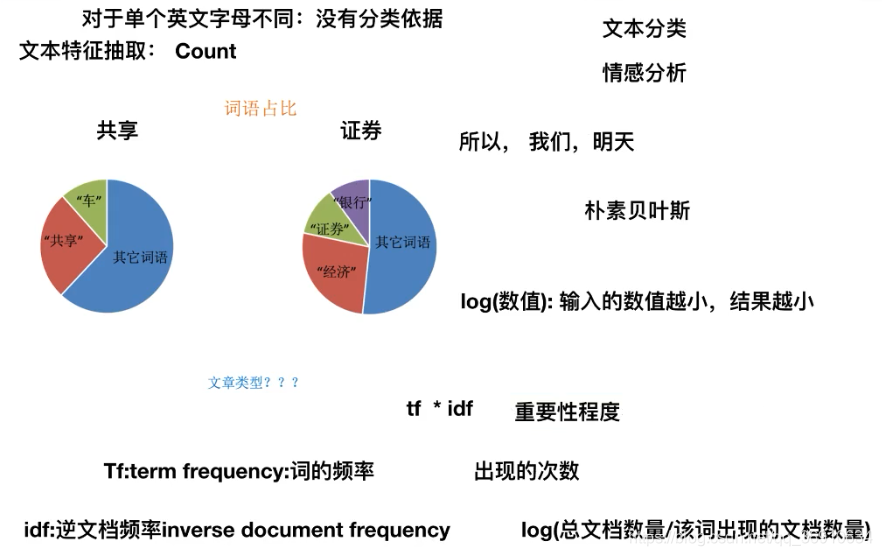
TF-IDF
TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的概率高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TF-IDF作用:用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
类:sklearn.feature_extraction.text.TfidfVectorizer
TfidfVectorizer语法
•TfidfVectorizer(stop_words=None,…)
•返回词的权重矩阵
•TfidfVectorizer.fit_transform(X,y)
•X:文本或者包含文本字符串的可迭代对象
•返回值:返回sparse矩阵
•TfidfVectorizer.inverse_transform(X)
•X:array数组或者sparse矩阵
返回值:转换之前数据格式
•TfidfVectorizer.get_feature_names()
•返回值:单词列表
- def tfidfvec():
- """
- 中文特征值化
- :return: None
- """
- c1, c2, c3 = cutword()
-
- print(c1, c2, c3)
-
- tf = TfidfVectorizer()
-
- data = tf.fit_transform([c1, c2, c3])
-
- print(tf.get_feature_names())
-
- print(data.toarray())
-
- return None
-
-
- if __name__ == "__main__":
- tfidfvec()

特征处理是什么
通过特定的统计方法(数学方法)将数据转换成算法要求的数据
数值型数据:标准缩放:
1、归一化
2、标准化
3、缺失值
类别型数据:one-hot编码
时间类型:时间的切分
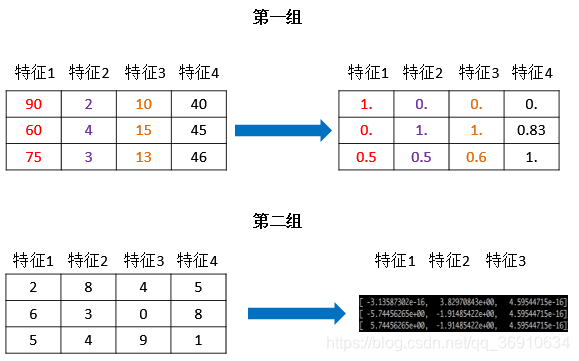
归一化
特点:通过对原始数据进行变换把数据映射到(默认为[0,1])之间
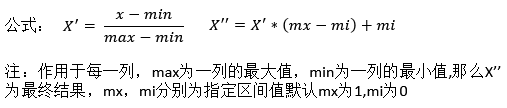
归一化公式计算过程
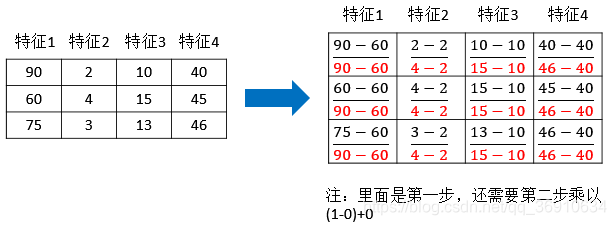
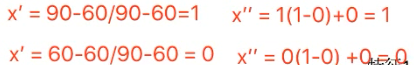
sklearn归一化API: sklearn.preprocessing.MinMaxScaler
MinMaxScaler语法
•MinMaxScalar(feature_range=(0,1)…)
•每个特征缩放到给定范围(默认[0,1])
•MinMaxScalar.fit_transform(X)
•X:numpy array格式的数据[n_samples,n_features]
•返回值:转换后的形状相同的array
- def mm():
- """
- 归一化处理
- :return: None
- """
- mm = MinMaxScaler(feature_range=(2, 3)) # 默认0-1范围
-
- data = mm.fit_transform([[90,2,10,40],[60,4,15,45],[75,3,13,46]])
-
- print(data)
-
- return None
-
-
- if __name__ == "__main__":
- mm()

为什么要进行归一化
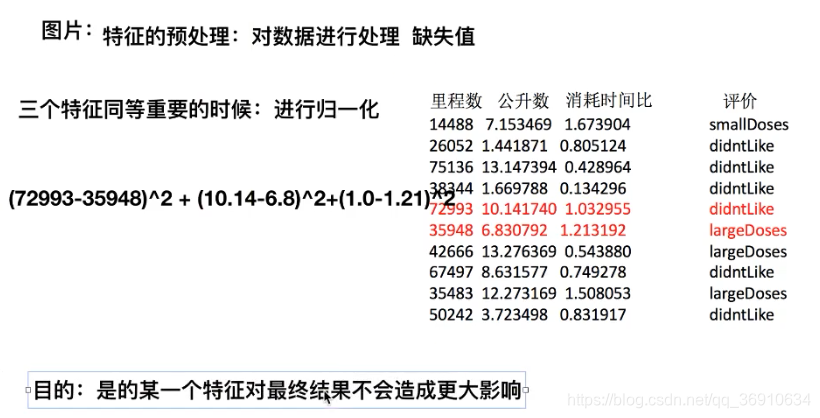
问题:如果数据中异常点较多,会有什么影响?

归一化总结
注意在特定场景下最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性(稳定性)较差,只适合传统精确小数据场景。
标准化
1、特点:通过对原始数据进行变换把数据变换到均值为0,方差为1范围内

方差越小点越密集,数据越稳定,当方差=0,所有数据都相等
结合归一化来谈标准化
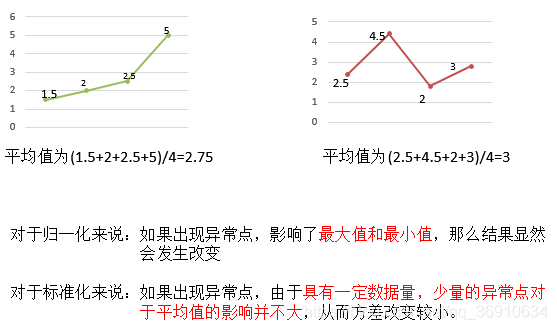
sklearn特征化API: scikit-learn.preprocessing.StandardScaler
StandardScaler语法
•StandardScaler(…)
•处理之后每列来说所有数据都聚集在均值0附近方差为1
•StandardScaler.fit_transform(X,y)
•X:numpy array格式的数据[n_samples,n_features]
•返回值:转换后的形状相同的array
•StandardScaler.mean_
•原始数据中每列特征的平均值
•StandardScaler.std_
•原始数据每列特征的方差
- def stand():
- """
- 标准化缩放
- :return:
- """
- std = StandardScaler()
-
- data = std.fit_transform([[ 1., -1., 3.],[ 2., 4., 2.],[ 4., 6., -1.]])
-
- print(data)
-
- return None
-
- if __name__ == "__main__":
- stand()

标准化总结
在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。
缺失值处理方法

Imputer语法
•Imputer(missing_values='NaN', strategy='mean', axis=0)
•完成缺失值插补
•Imputer.fit_transform(X,y)
•X:numpy array格式的数据[n_samples,n_features]
•返回值:转换后的形状相同的array
- def im():
- """
- 缺失值处理
- :return:NOne
- """
- # NaN, nan
- im = Imputer(missing_values='NaN', strategy='mean') # 使用Imputer则参数可以是np.nan或者'NaN'
- im2 = SimpleImputer(missing_values=np.nan, strategy='mean') # 使用SimpleImputer则参数必须是np.nan,否则报错
-
- data = im.fit_transform([[1, 2], [np.nan, 3], [7, 6]])
- data2 = im2.fit_transform([[1, 2], [np.nan, 3], [7, 6]])
-
- print(data)
- print(data2)
-
- return None
-
-
- if __name__ == "__main__":
- im()
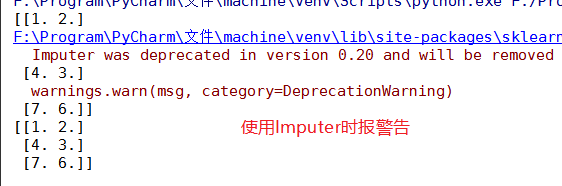
关于np.nan(np.NaN)
1、 numpy的数组中可以使用np.nan/np.NaN来代替缺失值,属于float类型
2、如果是文件中的一些缺失值,可以替换成nan,通过np.array转化成float型的数组即可
特征选择原因
•冗余:部分特征的相关度高,容易消耗计算性能
•噪声:部分特征对预测结果有负影响
特征选择是什么
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后可以改变值、也不改变值,但是选择后的特征维数肯定比选择前小,毕竟我们只选择了其中的一部分特征。
主要方法(三大武器):
Filter(过滤式):VarianceThreshold
Embedded(嵌入式):正则化、决策树
Wrapper(包裹式)
VarianceThreshold语法
•VarianceThreshold(threshold = 0.0)
•删除所有低方差特征
•Variance.fit_transform(X,y)
•X:numpy array格式的数据[n_samples,n_features]
•返回值:训练集差异低于threshold的特征将被删除。
•默认值是保留所有非零方差特征,即删除所有样本
•中具有相同值的特征。
- def var():
- """
- 特征选择-删除低方差的特征
- :return: None
- """
- var = VarianceThreshold(threshold=1.0)
-
- data = var.fit_transform([[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]])
-
- print(data)
- return None
-
-
- if __name__ == "__main__":
- var()
PCA(主成分分析)是什么
本质:PCA是一种分析、简化数据集的技术
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量

高维度数据容易出现的问题
•特征之间通常是线性相关的

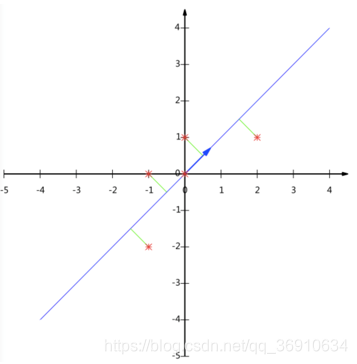
二维简化成一维,且数据不减少
通过公式计算(只做了解)

PCA语法
•PCA(n_components=None)
•将数据分解为较低维数空间
•PCA.fit_transform(X)
•X:numpy array格式的数据[n_samples,n_features]
•返回值:转换后指定维度的array

- def pca():
- """
- 主成分分析进行特征降维
- :return: None
- """
- pca = PCA(n_components=0.9)
-
- data = pca.fit_transform([[2,8,4,5],[6,3,0,8],[5,4,9,1]])
-
- print(data)
-
- return None
-
-
- if __name__ == "__main__":
- pca()

</div>